Unordered Close Following Agents

Agent-Close Following is an edge cose in mutual exclusive resource allocation, i.e. the same resource can be hold by at most one agent at the same time. In Flatland, grid cell is a resource, and only one agent can be in a grid cell. The only exception are level-free crossings, where there is horizontal and a vertical resource at the same grid cell.

The naive solution to this problem is to iterate among all agents, verify that their targeted resource is not occupied, if so allow the movement, else stop the agent. However, when agents follow each other in chain of cells, different agent orderings lead to different decisions under this algorithm.

MotionCheck ensures:

• no swaps (i.e. collisions)

• no two agents must be allowed to move to the same target cell (resource)

• if all agents in the chain run at the same speeed, all can run (behaviour not depending on agent indices)

%load_ext autoreload
%autoreload 2
from IPython import display 
display.display(display.HTML("<style>.container { width:95% !important; }</style>"))

import networkx as nx
import PIL
from IPython import display
import time
from matplotlib import pyplot as plt
import numpy as np
import sys
sys.executable

'/opt/hostedtoolcache/Python/3.10.17/x64/bin/python'

from flatland.envs import malfunction_generators as malgen
from flatland.envs.agent_utils import EnvAgent
from flatland.envs import rail_generators as rail_gen
from flatland.envs import agent_chains as ac
from flatland.envs.rail_env import RailEnv, RailEnvActions
from flatland.envs.persistence import RailEnvPersister
from flatland.utils.rendertools import RenderTool
from flatland.utils import env_edit_utils as eeu
from flatland.utils import jupyter_utils as ju
from tests.test_agent_chains import create_test_agents2

agents = {
    # stopped chain
    0: ((1, 0), (1, 1)),
    1: ((1, 1), (1, 2)),
    2: ((1, 2), (1, 3)),
    3: ((1, 3), (1, 3)),

    # running chain
    4: ((2, 0), (2, 1)),
    5: ((2, 1), (2, 2)),
    6: ((2, 2), (2, 3)),
    7: ((2, 3), (2, 4)),

    # stopped short chain
    8: ((3, 0), (3, 1)),
    9: ((3, 1), (3, 1)),

    # swap
    10: ((4, 1), (4, 2)),
    11: ((4, 2), (4, 1)),

    # mid-chain stop
    12: ((5, 1), (5, 2)),
    13: ((5, 2), (5, 3)),
    14: ((5, 3), (5, 2)),
    15: ((6, 1), (6, 2)),
    16: ((6, 2), (6, 3)),
    17: ((6, 3), (6, 4)),
    18: ((6, 4), (6, 4)),
    19: ((6, 5), (6, 6)),
    20: ((6, 6), (6, 7)),

    # mid-chain swap
    21: ((7, 1), (7, 2)),
    22: ((7, 2), (7, 3)),
    23: ((7, 3), (7, 4)),
    24: ((7, 4), (7, 3)),
    25: ((7, 5), (7, 4)),
    26: ((7, 6), (7, 5)),

    # land on same
    27: ((8, 1), (8, 2)),
    28: ((8, 3), (8, 2)),

    # chains onto same
    29: ((9, 1), (9, 2)),
    30: ((9, 2), (9, 3)),
    31: ((9, 3), (9, 4)),
    32: ((9, 5), (9, 4)),
    33: ((9, 6), (9, 5)),
    34: ((9, 7), (9, 6)),

    # 3-way same
    35: ((10, 1), (10, 2)),
    36: ((10, 3), (10, 2)),
    37: ((11, 2), (10, 2)),

    # tee
    38: ((12, 1), (12, 2)),
    39: ((12, 2), (12, 3)),
    40: ((12, 3), (12, 4)),
    41: ((13, 3), (12, 3)),

    # tree
    42: ((14, 1), (14, 2)),
    43: ((14, 2), (14, 3)),
    44: ((14, 3), (14, 4)),
    45: ((15, 3), (14, 3)),
    46: ((15, 2), (15, 3)),
    47: ((16, 2), (15, 3)),
    48: ((18, 3), (17, 3)),
    49: ((18, 2), (18, 3)),
    50: ((19, 2), (18, 3)),
    51: ((17, 1), (17, 2)),
    52: ((17, 2), (17, 3)),
    53: ((17, 3), (17, 4)),
}
expected = {0: False, 1: False, 2: False, 3: False, 4: True, 5: True, 6: True, 7: True, 8: False, 9: False, 10: False, 11: False, 12: False, 13: False,
            14: False, 15: False, 16: False, 17: False, 18: False, 19: True, 20: True, 21: False, 22: False, 23: False, 24: False, 25: False, 26: False,
            27: True, 28: False, 29: True, 30: True, 31: True, 32: False, 33: False, 34: False, 35: True, 36: False, 37: False, 38: True, 39: True,
            40: True, 41: False, 42: True, 43: True, 44: True, 45: False, 46: False, 47: False, 48: True, 49: True, 50: False, 51: False, 52: False,
            53: True}

G = nx.DiGraph()
edge_labels = {}
edge_colors_map = {}
node_color_map = {}
for i, (u,v) in agents.items():
    G.add_edge(u,v)
    edge_labels[(u,v)]=i
    edge_colors_map[(u,v)]= "red" if not expected[i] else "blue"
    node_color_map[u] = "red" if not expected[i] else "blue"

pos = {n:n for n in G.nodes}

node_color = [node_color_map[n] if n in node_color_map else "blue" for n in G.nodes]

edge_colors = [edge_colors_map[e] for e in G.edges]

fig, ax = plt.subplots(figsize=(30, 10))
nx.draw(G, pos=pos, with_labels=True,ax=ax, edge_color=edge_colors,connectionstyle="arc3,rad=0.1",arrowsize=20, node_color=node_color)
nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels, font_size=15)
plt.show()

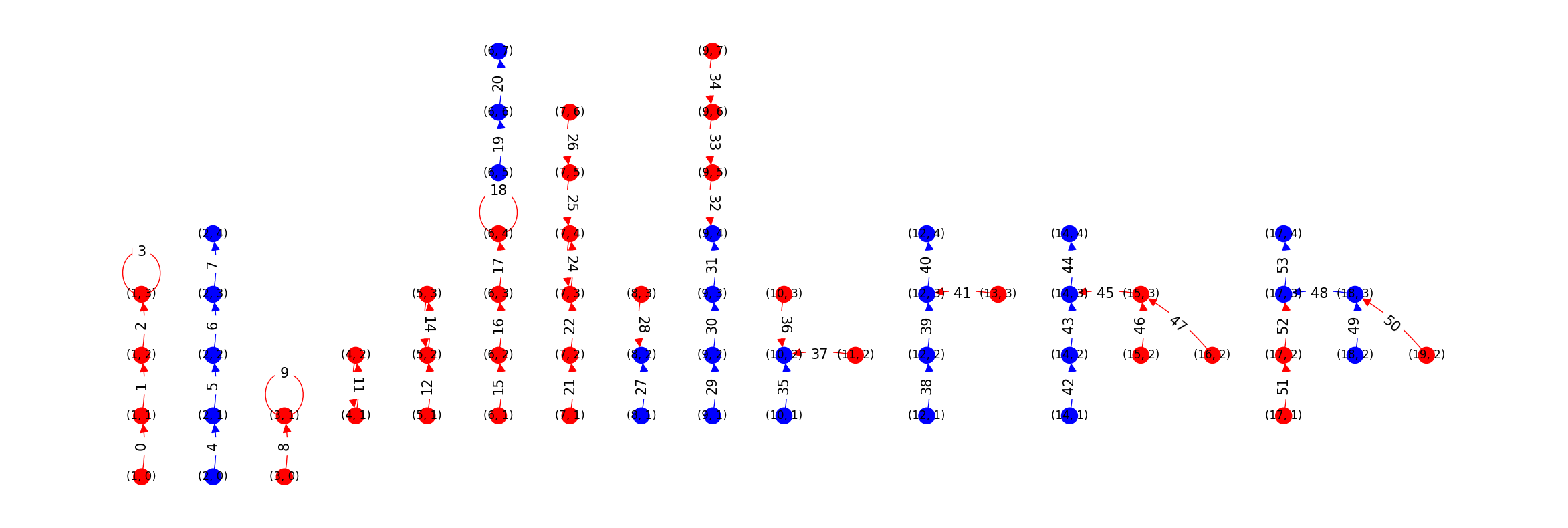
Arrows represent the desired movement of agents.

Edges got from the agent’s current position (cell as row-column pair) to the desired target position, and the edge label is the agent ID.

Self-loops represent agents not wanting to move - additionally the corresponding node is also marked red.

Red edges represent agents which are stopped by motion check or which do not want to move (if self-loop) - the corresponding start cell is also marked red.